Bitcoin is not Anonymous
Bitcoin is not inherently anonymous. It may be possible to conduct transactions is such a way so as to obscure your identity, but, in many cases, users and their transactions can be identified. We have performed an analysis of anonymity in the Bitcoin system and published our results in a preprint on arXiv.
The Full Story
Anonymity is not a prominent design goal of Bitcoin. However, Bitcoin is often referred to as being anonymous. We have performed a passive analysis of anonymity in the Bitcoin system using publicly available data and tools from network analysis. The results show that the actions of many users are far from anonymous. We note that several centralized services, e.g. exchanges, mixers and wallet services, have access to even more information should they wish to piece together users' activity. We also point out that an active analysis, using say marked Bitcoins and collaborating users, could reveal even more details. The technical details are contained in a preprint on arXiv. We welcome any feedback or corrections regarding the paper.
Case Study: The Bitcoin Theft
To illustrate our findings, we have chosen a case study involving a user who has many reasons to stay anonymous. He is the alleged thief of 25,000 Bitcoins. This is a summary of the victim's postings to the Bitcoin forums and an analysis of the relevant transactions.
Summary
The victim woke up on the morning of 13/06/2011 to find a large portion of his Bitcoins sent to 1KPTdMb6p7H3YCwsyFqrEmKGmsHqe1Q3jg. The alleged theft occurred on 13/06/2011 at 16:52:23 UTC shortly after somebody broke into the victim's Slush pool account and changed the payout address to 15iUDqk6nLmav3B1xUHPQivDpfMruVsu9f. The Bitcoins rightfully belong to 1J18yk7D353z3gRVcdbS7PV5Q8h5w6oWWG.
An Egocentric Analysis
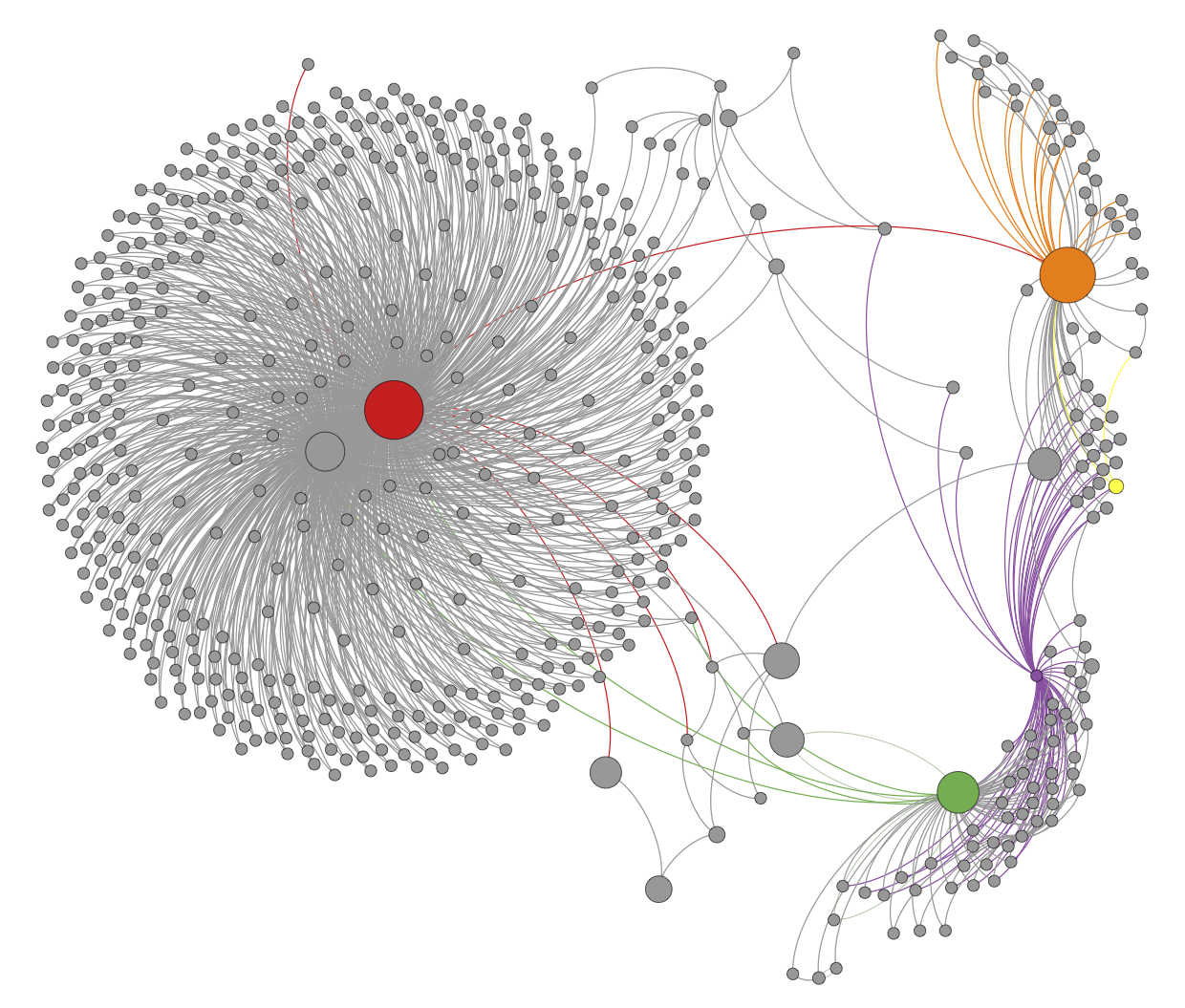
Fig. 1: The egocentric user network of the thief.
We consider the user network of the thief. Each vertex represents a user and each directed edge between a source and a target represents a flow of Bitcoins from a public-key belonging to the user corresponding to the source to a public-key belonging to the user corresponding to the target. Each directed edge is colored by its source vertex. The network is imperfect in the sense that there is, at the moment, a one-to-one mapping between users and public-keys. We restrict ourselves to the egocentric network surrounding the thief: we include every vertex that is reachable by a path of length at most two ignoring directionality and all edges induced by these vertices. We also remove all loops, multiple edges and edges that are not contained in some biconnected component to avoid clutter. In Fig. 1, the red vertex represents the thief and the green vertex represents the victim. The theft is the green edge joining the victim and the thief. There are in fact two green edges located nearby in Fig. 1 but only one directly connects the victim to the thief.
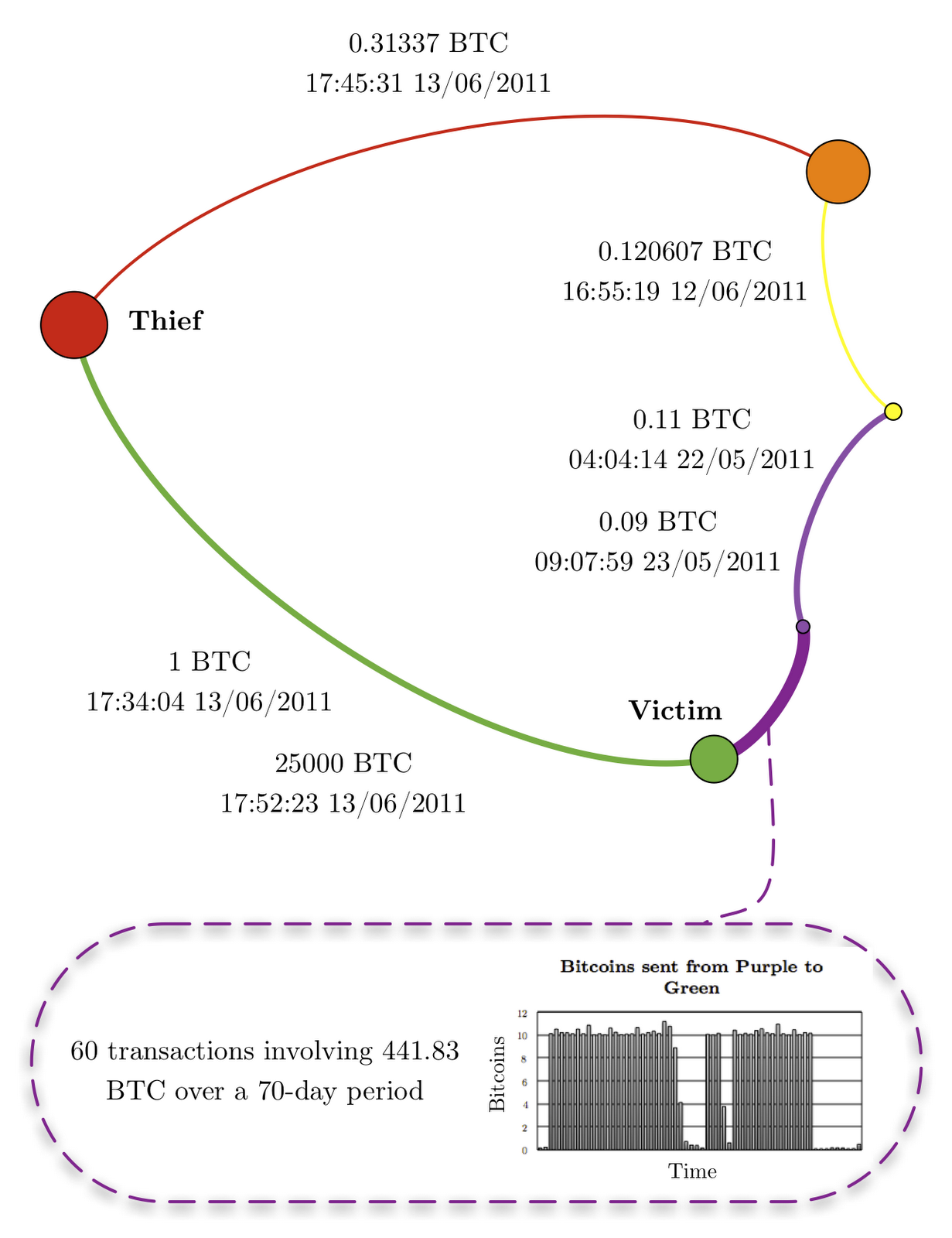
Fig. 2: An interesting sub-network induced by the thief, the victim and three other vertices.
Interestingly, the victim and the thief are joined by paths (ignoring directionality) other than the green edge representing the theft. For example, consider the sub-network shown in Fig. 2 induced by the red, green, purple, yellow and orange vertices. This sub-network is a cycle. We contract all vertices whose corresponding public-keys belong to the same user. This allows us to attach values in Bitcoins and timestamps to the directed edges. Firstly, we note that the theft of 25,000 BTC was preceded by a smaller theft of 1 BTC. This was later reported by the victim in the Bitcoin forums. Secondly, using off-network data, we have identified some of the other colored vertices: the purple vertex represents the main Slush pool account and the orange vertex represents the computer hacker group LulzSec (see, for example, their Twitter stream). We note that there has been at least one attempt to associate the thief with LulzSec. This was a fake; it was created after the theft. However, the identification of the orange vertex with LulzSec is genuine and was established before the theft. We observe that the thief sent 0.31337 BTC to LulzSec shortly after the theft but we cannot otherwise associate him with the group. The main Slush pool account sent a total of 441.83 BTC to the victim over a 70-day period. It also sent a total of 0.2 BTC to the yellow vertex over a 2-day period. One day before the theft, the yellow vertex also sent 0.120607 BTC to LulzSec. The yellow vertex represents a user who is the owner of at least five public-keys:
* 1MUpbAY7rjWxvLtUwLkARViqSdzypMgVW4
* 13tst9ukW294Q7f6zRJr3VmLq6zp1C68EK
* 1DcQvXMD87MaYcFZqHzDZyH3sAv8R5hMZe
* 1AEW9ToWWwKoLFYSsLkPqDyHeS2feDVsVZ
* 1EWASKF9DLUCgEFqfgrNaHzp3q4oEgjTsF
Like the victim, he is a member of the Slush pool, and like the thief, he is a one-time donator to LulzSec. This donation, the day before the theft, is his last known activity using these public-keys.
A Flow and Temporal Analysis
In addition to visualizing the egocentric network of the thief with a fixed radius, we can follow significant flows of value through the network over time. If a vertex representing a user receives a large volume of Bitcoins relative to their estimated balance, and, shortly after, transfers a significant proportion of those Bitcoins to another user, we deem this interesting. We built a special purpose tool that, starting with a chosen vertex or set of vertices, traces significant flows of Bitcoins over time. In practice we have found this tool to be quite revealing when analyzing the user network.
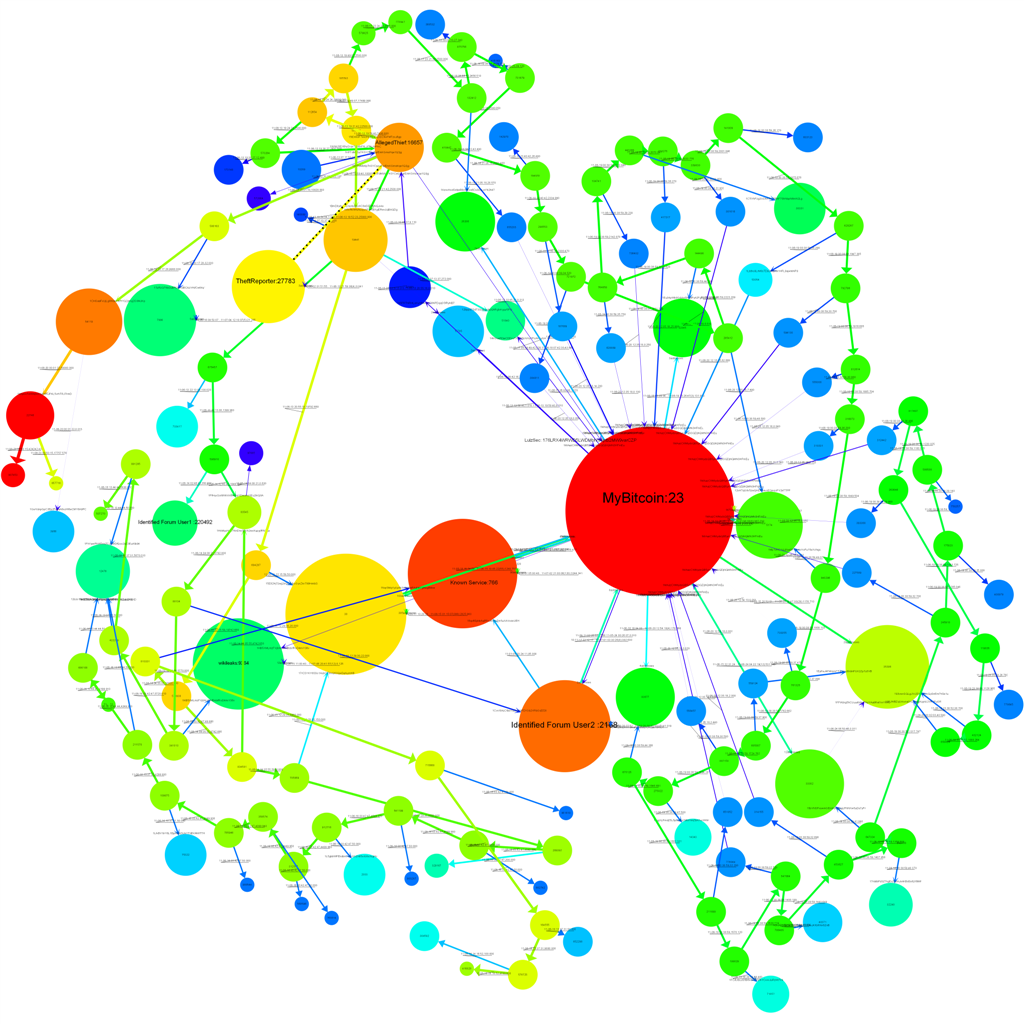
Fig. 3: A visualization of Bitcoin flow from the theft. The size of a vertex corresponds to its degree in the entire network. The color denotes the volume of Bitcoins — warmer colors have larger volumes flowing through them. We also provide an SVG which contains hyperlinks to the relevant Block Explorer pages.
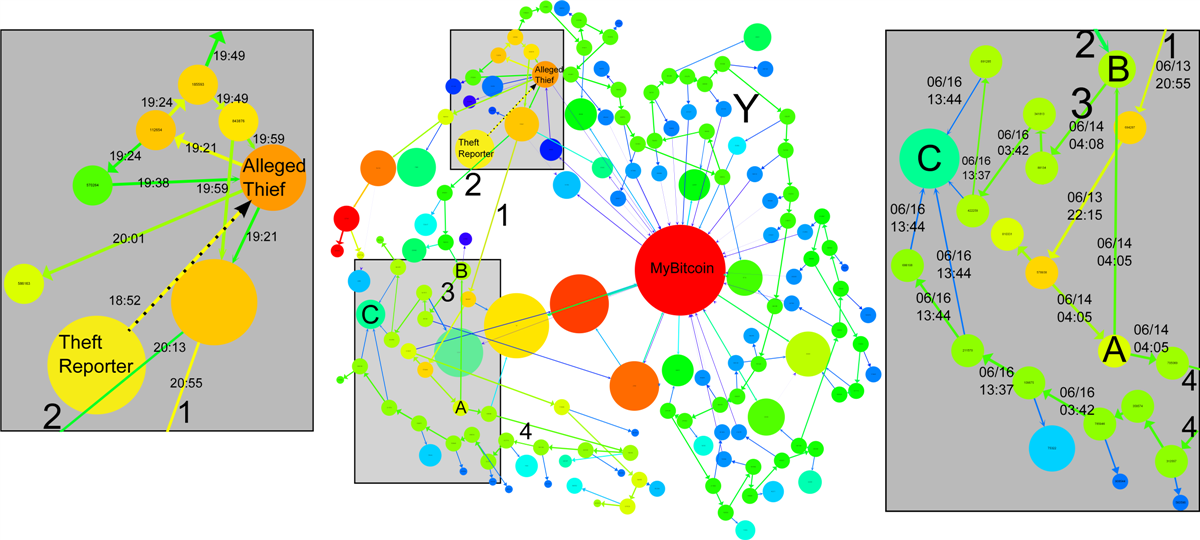
Fig. 4: An annotated version of Fig. 3.
In the left inset, we can see that the Bitcoins are shuffled between a small number of accounts and then transferred back to the initial account. After this shuffling step, we have identified four significant outflows of Bitcoins that began at 19:49, 20:01, 20:13 and 20:55. Of particular interest are the outflows that began at 20:55 (labeled as 1 in both insets) and 20:13 (labeled as 2 in both insets). These outflows pass through several subsequent accounts over a period of several hours. Flow 1 splits at the vertex labeled A in the right inset at 04:05 the day after the theft. Some of its Bitcoins rejoin Flow 2 at the vertex labeled B. This new combined flow is labeled as 3 in the right inset. The remaining Bitcoins from Flow 1 pass through several additional vertices in the next two days. This flow is labeled as 4 in the right inset.
A surprising event occurs on 16/06/2011 at approximately 13:37. A small number of Bitcoins are transferred from Flow 3 to a heretofore unseen public-key 1FKFiCYJSFqxT3zkZntHjfU47SvAzauZXN. Approximately seven minutes later, a small number of Bitcoins are transferred from Flow 3 to another heretofore unseen public-key 1FhYawPhWDvkZCJVBrDfQoo2qC3EuKtb94. Finally, there are two simultaneous transfers from Flow 4 to two more heretofore unseen public-keys: 1MJZZmmSrQZ9NzeQt3hYP76oFC5dWAf2nD and 12dJo17jcR78Uk1Ak5wfgyXtciU62MzcEc. We have determined that these four public-keys — which receive Bitcoins from two separate flows that split from each other two days previously — are all contracted to the same user in our ancillary network. This user is represented as C.
There are several other examples of interesting flow. The flow labeled as Y involves the movement of Bitcoins through thirty unique public-keys in a very short period of time. At each step, a small number of Bitcoins (typically 30 BTC which had a market value of approximately US$500 at the time of the transactions) are siphoned off. The public-keys that receive the small number of Bitcoins are typically represented by small blue vertices due to their low volume and degree. On 20/06/2011 at 12:35, each of these public-keys makes a transfer to a public-key operated by the MyBitcoin service. Curiously, this public-key was previously involved in another separate Bitcoin theft.
Conclusion
This is a straight-forward passive analysis of public data that allows us to de-anonymize considerable portions of the Bitcoin network. We can use tools from network analysis to visualize egocentric networks and to follow the flow of Bitcoins. This can help us identify several centralized services that may have even more details about interesting users. We can also apply techniques such as community finding, block modeling, network flow algorithms, etc. to better understand the network.
Feedback
We are excited about the Bitcoin project and consider it a remarkable milestone in the evolution of electronic currencies. Our motivation for this work has not been to de-anonymize any individual users; rather it is to illustrate the limits of anonymity in the Bitcoin system. It is important that users do not have a false expectation of anonymity. We welcome any feedback or comments regarding the preprint on arXiv or the details in this post.
This research was done by Fergal Reid and Martin Harrigan
Bitcoin Mixers and Tumblers List:

Sinbad acts as an bitcoin tumbler or mixing service that mixes your coins with other users' funds and pay out in multiple randomized transactions to further anonymize the source of money.
READ REVIEWS VISIT WEBSITE
Blender.io is an anonymous bitcoin mixing service launched in 2022. Its purpose is to help other people stay anonymous. Coin control is used to make sure you are not receiving the same bitcoins as deposited.
READ REVIEWS VISIT WEBSITE
Cryptomixer does not just clean your bitcoins it gives you brand new freshly mined uncirculated bitcoins. The Cryptomixer's system is more than a simple bitcoin tumbler, it is privacy and security wrapped in one.
READ REVIEWS VISIT WEBSITE